Isohedra

Regular Tetrahedron (D)

N=4, M=3, R=3, V=4, E=6

[3,3,3],aaa

Only one type of vertex with 3 edges.

Platonic solid

 ?or?

Regular Trigonal Dipyramid (I)

N=6, M=3, M1=2, R1=4, V1=3, M2=1, R2=3, V2=2

[4,4,3],aab

1 doublet plus 1 singlet corner.

The singlet and doublet corners are part of different types of vertices.

This is a special case where the triangles are equilateral. However, there are still two different vertex types (and thus this is not a Platonic solid).

Regular Octahedron

(E)

N=8, M=3, R=4, V=6, E=12

[4,4,4],aaa

Only one type of vertex with 4 edges.

Platonic solid, dual of the cube.

Regular Pentagonal Dipyramid (I)

N=10, M=3, M1=2, R1=4, V1=5, M2=1, R2=5, V2=2

[4,4,5],aab

1 doublet plus 1 singlet corner.

The singlet and doublet corners are part of different types of vertices.

This is a special case where the triangles are equilateral. However, there are still two different vertex types (and thus this is not a Platonic solid).

Regular Icosahedron

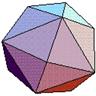
(F)

N=20, M=3, R=5, V=12, E=30

[5,5,5],aaa

Only one type of vertex with 5 edges.

Platonic solid, dual of the dodecahedron

Isosceles Tetrahedron / Tetragonal Disphenoid (D)

N=4, M=3, V=4, R=3, E=6

 [3,3,3],aab

1 doublet (a) plus 1 singlet (b) corner.

The singlet and doublet corners are part of the same type of vertex.

The Iscosceles Tetrahedron has only one type of vertex, but in each vertex one singlet and two doublet corners meet, satisfying Mogensen’s equation (8).

(Note: Mogensen [7] does not explicitly state that (D) need not be a regular tetrahedron)

Each edge is the diagonal of a cuboid

Triangular Dihedron / Double Pyramid / Bi-Pyramid / Di-Pyramid

 (I)

N even (N>=6), M=3, M1=2, R1=4, V1=N/2, M2=1, R2=N/2, V2=2

[4,4,N/2],aab

1 doublet (a) plus 1 singlet (b) corner.

The singlet and doublet corners are part of different types of vertices.

Opposing faces if N/2 even

Add loki3’s d6 - di-pyramid

N=6

Trigonal Dipyramid

N=8

Tetragonal Dipyramid

N=10

Pentagonal Dipyramid

N=12

Hexagonal Dipyramid

N=16

Octagonal Dipyramid

N=36

Octadecagonal Dipyramid

Triakis Tetrahedron / Tristetrahedron / Trigonal tristetrahedron,

(J)

N=12, V=8,E=18

M=3, M1=2, R1=6, V1=4, M2=1, R2=3, V2=4,

[3,6,6],abb

1 doublet (a) plus 1 singlet (b) corner.

The singlet and doublet corners are part of different types of vertices.

Triangular pyramids on tetrahedron faces, i.e., cumulation of the tetrahedron.

Catalan solid, dual of the truncated tetrahedron

Tetrakis Hexahedron / Tetrahexahedron

(K)

N=24, V=14, E=36

M=3, M1=2, R1=6, V1=8, M2=1, R2=4, V2=6,

[4,6,6], abb

1 doublet (a) plus 1 singlet (b) corner.

The singlet and doublet corners are part of different types of vertices.

 Square pyramids on cube faces, i.e., cumulation of the cube.

Catalan solid, dual of the truncated octahedron.

(Note: Mogensen [7] mentions octahedron instead of cube faces)

Triakis Octahedron / Small Triakis Octahedron/ Trisoctahedron / Trigonal Trisoctahedron

(M)

N=24, V=14, E=36

M=3, M1=2, R1=8, V1=6, M2=1, R2=3, V2=8,

[3,8,8], abb

1 doublet (a) plus 1 singlet (b) corner.

The singlet and doublet corners are part of different types of vertices.

Triagonal pyramids on octahedron faces, i.e., cumulation of the octahedron.

Catalan solid, dual of the truncated cube.

(Note: Mogensen [7] mentions cube instead of octahedron faces)

Pentakis Dodecahedron

(L)

N=60, V=32, E=90

M=3, M1=2, R1=6, V1=20, M2=1,R2=5, V2=12

[5,6,6],aab

1 doublet (a) plus 1 singlet (b) corner.

 The singlet and doublet corners are part of different types of vertices.

Pentagonal pyramids on dodecahedron faces, i.e., cumulation of the dodecahedron.

Catalan solid, dual of the truncated icosahedron.

Triakis Icosahedron

(N)

N=60, V=32, E=90

M=3, M1=2, R1=10, V1=12, M2=1, R2=3, V2=20

[3,10,10],aab

1 doublet (a) plus 1 singlet (b) corner.

The singlet and doublet corners are part of different types of vertices.

Triagonal pyramids on icosahedron faces, i.e., cumulation of the icosahedron.

Catalan solid      , dual of the truncated dodecahedron

Scalene tetrahedron / Rhombic disphenoid

(D)

N=4, M=3, R=3, V=4, E=6

[3,3,3],abg

3 singlet corners.

The three singlet corners are part of the same type of vertex.

The Scalene Tetrahedron has only one type of vertex, but in each vertex one each of the singlet corners meet, satisfying Mogensen’s equation (8).

(Note: Mogensen [7] does not explicitly state that (D) need not be a regular tetrahedron).

Each edge is the diagonal of a cuboid

Tetragonal Scalenohedron

N=8, M=3, M1=2, R1=4, V1=4, M2=1, R2=4, V2=2

3 singlet corners, yet only two types of vertices.

Same values as for a tetragonal Dipyramid (I), although composed of scalene triangles.

This is a shape of a family called Triangular Dihedron skewed up/down (D4n) which can be constructed by skewing the equatorial vertices of a dipyramid with 4n faces up and down.

"Scalenohedron" from the Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/Scalenohedron/

Skewed Triangular Dihedron / Double Pyramid / Bi-Pyramid / Di-Pyramid

(O)

N=8,12,16,.., M=3, M1=M2=M3=1, R1=R2=4, V1=V2=N/4, R3=N/2, V3=2

3 singlet corners, each is part of a different type of vertex.

deform variant of the Dipyramid (I)

This is a shape of a family called Triangular Dihedron skewed in/out (D4n) which can be constructed by squeezing the equatorial vertices of a dipyramid with 4n faces in and out from the center of the solid.

"Scalenohedron" from the Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/Scalenohedron/

missing

Hexakis Tetrahedron / Hextetrahedron

(P)

N=24, M=3, M1=1, R1=4, V1=6, M2=M3=1,R2=R3=6, V2=V3=4, V=14, E=36

[4,6,6],abg

3 singlet corners, each is part of a different type of vertice.

deform variant of (K)

(Note: Mogensen [7] incorrectly states that V1=4)

Hexakis Octahedron / Disdyakis Dodecahedron  / Hexoctahedron/ Octakis Hexahedron

(Q)

N=48, V=26, E=72

M=3, M1=1, R1=4, V1=12, M2=1, R2=6, V2=8, M3=1, R3=8, V3=6

[4,6,8],abg

3 singlet corners, each is part of a different type of vertice.

Rhombic pyramids on rhombic dodecahedron faces.

Catalan solid, dual of the truncated cuboctahedron

Hexakis Icosahedron / Disdyakis Triacontahedron

(R)

N=120, V=62, E=180

M=3, M1=1, R1=4, V1=30, M2=1, R2=6, V2=20, M3=1, R3=10, V3=12

[4,6,10],abg

3 singlet corners, each is part of a different type of vertice.

Largest non-bipolar die.

Rhombic pyramids on rhombic triacontahedron faces.

Catalan solid, , dual of the truncated icosidodecahedron.

Regular Hexahedron, Cube

(G)

N=6, M=4, R=3, V=8, E=12

[3,3,3,3],aaaa

Only one type of vertex with 3 edges.

Platonic solid, dual of the octahedron.

Rhombic Hexahedron,

Rhombohedron

(S)

N=6, M=4, M1=2, R1=3, V1=4, M2=2, R2=3, V2=4

[3,3,3,3], aaab

2 opposite doublet corners (a,b). Vertex type 2 consists of identical corners (b), vertex type 1 consists of different corners (a,a,b).

Deform variant of the Cube (G), special case of the Trapezohedron (V)

Note that it can be proven that there are no trapezohedra made of rhombi other than for N=6 (friz).

Rhombic Dodecahedron

(T)

N=12, V=14, E=24

M=4, M1=2, R1=3, V1=8, M2=2, R2=4, V2=6

[3,4,3,4],abab

2 opposite doublet corners (a,b), each is part of a different type of vertice.

Catalan solid, dual of the cuboctahedron.

Rhombic Triacontahedron

(U)

N=30, V=32, E=60

M=4, M1=2, R1=3, V1=20, M2=2, R2=5, V2=12

[3,5,3,5],abab

2 opposite doublet corners (a,b), each is part of a different type of vertice.

Catalan solid, dual of the icosidodecahedron

Trapezoidal Dihedron / Trapezohedron / Antidipyramids / Deltohedron

Crystallographic examples: Tetragonal Trapezohedron (N=8), Hexagonal Trapezohedron (N=12)

(V)

N even (N>6), V=N+2, E=2N

M=4, M1=3, R1=3, V1=N, M2=1, R2=N/2, V2=2

[3,3,3,N/2],aaab

1 doublet and 2 singlet corners, doublet and one of the singlets are part of the same type of vertex

double cone made from kites

opposing faces if N/2 odd

"Streptohedron and Trapezohedron" from the Wolfram Demonstrations Project
 http://demonstrations.wolfram.com/StreptohedronAndTrapezohedron/

Note that it can be proven that there is no Trigonal Trapezohedron (N=6) composed of deltoids (proof by friz). The faces have to be squares (a cube), rhombi (a rhombic cube) or irregular quadrilaterals.

N=8

Tetragonal Trapezohedron

N=10

Pentagonal Trapezohedron

N=12

Hexagonal Trapezohedron

N=14

Heptagonal Trapezohedron

N=18

Enneagonal Trapezohedron

N=26

Trisdecagonal Trapezohedron

N=34

Heptadecagonal Trapezohedron

N=50

Icosikaipentagonal Trapezohedron

Deltoidal Dodecahedron / Trapezoidal Dodecahedron / Trapezohedral Tristetrahedron

(W)

N=12, M=4, M1=2, R1=4, V1=6, M2=M3=1, R2=R3=3, V2=V3=4, V=14, E=24

[3,4,3,4],abgb

1 doublet (a) and 2 singlet (b,c) corners, doublet and both singlets all form their own vertices.

deform variant of the rhombic dodecahedron (T)

Deltoidal Icositetrahedron / Trapezoidal Icositetrahedron / Strombic Icositetrahedron / Trapezohedral Trisoctahedron / Trapezohedron,

(X)

N=24, V=26, E=48

M=4, M1=2, R1=4, V1=12, M2=1, R2=3, V2=8, M3=1, R3=4, V3=6

[3,4,4,4],abgb

1 doublet and 2 singlet corners, doublet and both singlets all form their own vertices.

Can be made by replacing each face of a cube with four kites.

Catalan solid, dual of the rhombicuboctahedron

Deltoidal Hexecontahedron / Trapezoidal Hexecontahedron / Strombic Hexecontahedron

(Y)

N=60, V=62, E=120

M=4, M1=2, R1=4, V1=30, M2=1, R2=3, V2=20, M3=1, R3=5, V3=12

[3,4,5,4],abgb

1 doublet and 2 singlet corners, doublet and both singlets all form their own vertices.

Can be made by replacing each face of a regular dodecahedron  with five kites.

Catalan solid, dual of the rhombicosidodecahedron.

Skewed Trapezoidal Dihedron / Trapezohedron / Antidipyramids / Deltohedron

deform variant of the Trapezohedron (V)

N even (N>=6), M=4, M1=3, R1=3, V1=N, M2=1, R2=N/2, V2=2

4 singlet corners, but only 2 types of vertices. Vertex type 2 consists of identical corners (a), vertex type 1 consists of different corners (b,c,d).

Examples:

Skewed Trigonal Trapezohedron (N=6)

Lengths a-d and a-b are identical.

Skewed Hexagonal Trapezohedron (N=12)

Lengths a-d and a-b are identical.

Skewed Rhombic Dodecahedron

N=12, M=4, R1=4, V1=6, R2=R3=3, V2=V3=4

deform variant of (W)

4 singlet corners, but only 3 types of vertices. Vertex type 1 consists of identical corners (a), vertex type 2 consists of corners (b,b,c), vertex type 3 consists of corners (c,d,d).

Length b-c and c-d are identical

??? missing in loki3’s table???

Dyakis Dodecahedron / Didodecahedron / Diploid

N=24, M=4, M1=2, R1=4, V1=12, M2=1, R2=3, V2=8, M3=1, R3=4, V3=6, V=26, E=48

[3,4,4,4],aabg

Two adjacent sides are equal.

deform variant of the Deltoidal Icositetrahedron (X)

missing

Skewed Deltoidal Hexecontahedron

N=60, M=4, R1=4, V1=30, R2=3, V2=20, R3=5, V3=12

deform variant of (Y)

??? missing in loki3’s table???

Regular (Pentagonal) Dodecahedron

(H)

N=12, M=5, R=3, V=20, E=30

[3,3,3,3,3],aaaaa

Only one type of vertex with 3 edges.

Platonic solid, dual of the icosahedron

Octahedral Pentagonal Dodecahedron /

Pentagonal Dodecahedron /

Pyritohedron

 (Z)

N=12, M=5, M1=3, R1=3, V1=12, M2=2, R2=3, V2=8, V=20, E=30

[3,3,3,3,3],abbbb

2 doublets and 1 singlet, one doublet and the singlet are part of the same type of vertex.

A deform dodecahedron which has a symmetry that mirrors the octahedron.

Note that 4 edges of the pentagon are of equal length with bilateral symmetry. The vertices of Type 2 form a cube.

include pix w/ corners

Tetragonal Pentagonal Dodecahedron / Tetartoid

(Æ)

N=12, M=5, M1=3, R1=3, V1=12, M2=M3=1, R2=R3=3, V2=V3=4, V=20, E=30

[3,3,3,3,3],abbgg

All singlet corner types, one type of vertex with three corner types, and two vertices with one corner type.

Skewed dodecahedron which looks similar to the Tetrahedron.

There are no parallel faces. The design by loki3 consists of a wireframe with embedded parallel sides.

Pentagonal Icositetrahedron / Pentagon Trioctahedron /  Gyroid

(Ø)

N=24, M=5, M1=3, R1=3, V1=24, M2=1, R2=3, V2=8, M3=1, R3=4, V3=6, V=38, E=60

 [3,3,3,3,4],abbgg

Two pairs of equal adjacent sides

All singlet corner types, one type of vertex with three corner types, and two vertices with one corner type.

Can be made by placing sets of four pentagons on each face of a cube, turned a bit to make the corners interlace.

No parallel faces.

Catalan solid, dual of the snub cube

Both enantiomorphous forms, known as laevo (left) and dextro (right) have the same edge code since they are mirror since they are mirror image versions of each other (thanks to loki3 for the hint)

Pentagonal Hexecontahedron

(Å)

N=60, M=5, M1=3, R1=3, V1=60, M2=1, R2=3, V=20, M3=1, R3=5, V3=12, V=92, E=150

[3,3,3,3,5],abbgg

All singlet corner types, one type of vertex with three corner types, and two vertices with one corner type.

Can be made by placing sets of five pentagons on each face of a dodecahedron, turned a bit to make the corners interlace.

No parallel faces.

Catalan solid, , dual of the snub dodecahedron.

Both enantiomorphous forms, known as laevo (left) and dextro (right) have the same edge code since they are mirror image versions of each other (thanks to loki3 for the hint)